本文章整理了沈黄晋所著的《大学物理学（下）》中光学的部分。

本文章主要包含以下章节内容：

几何光学（仅包含折射定律）
光的干涉
光的衍射
光的偏振

折射定律

\frac{\sin i}{\sin r} = \frac{n_2}{n_1} = n_{12}

n_{12} 表示2相对1的折射率，注意折射定律n2和n1是反着的就行（记忆方法：空角大，相对真空的折射率都是大于1的数）。

同时注意

n = \frac c u

光的干涉

光的叠加

此处具体推导过程省略

两点光振动方程：

E_1(t) = E_{m1}cos[\omega t+\varphi_{10}(t)] \\ E_2(t) = E_{m2}cos[\omega t+\varphi_{20}(t)]

在P点的光振动：

E_{1P}(r_1,t) = E_{m1}cos[\omega t+\varphi_{10}(t)-\frac{2\pi}{\lambda}r_1]

E_{2P}(r_2,t) = E_{m2}cos[\omega t+\varphi_{20}(t)-\frac{2\pi}{\lambda}r_2]

叠加强度：

E_{P0} = \sqrt{E_{10}^2+E_{20}^2+2E_{10}E_{20}cos{\Delta\varphi_P}}

相位差：

\Delta\varphi_P=\varphi_{20}(t)-\varphi_{10}(t)-\frac{2\pi}{\lambda}(r_2-r_1)

非相干叠加由于不是两束相干光无法形成稳定的干涉图案，此处讨论相干叠加：

显然，cos项取+1和-1分别对应最大最小值：

当 \Delta\varphi_P=\pm 2k\pi , k=0,1,2,... ：

E_{P0} = E_{max} = E_{10} + E_{20} \\ I=I_{max} = (E_{10} + E_{20})^2

当 \Delta\varphi_P=\pm (2k-1)\pi , k=0,1,2,... ：

E_{P0} = E_{min} = |{E_{10} - E_{20}}| \\ I=I_{min} = (E_{10} - E_{20})^2

干涉条纹对比度：

\eta = \frac{I_{max}-I_{min}}{I_{max}+I_{min}}

0对应非相干叠加，1对应对比度最强的相干叠加。

分波阵面法产生干涉

杨氏双缝干涉

不是很想背书上的公式，可以按照光栅方程去背：

d\sin\theta = \pm k\lambda

其中

\sin \theta = \frac x D

条件啥的都很容易求得，这里不过多赘述。

光程和光程差的概念应该也很好理解。

剩下两种干涉的计算方式是相同的，只是使用了不同的实验结构，但是上述的公式仍然成立。

其中特别强调劳埃德镜实验主要证明了半波损失。

分振幅法产生光的干涉

薄膜干涉的计算较为复杂，此处直接给出最终结果：

\delta_0 = 2e\sqrt{n_2^2-n_1^2\sin^2i} \\ \delta_0 = 2n_2e\cos\gamma

同时还要考虑反射引起的附加光程差，这里手推一下就行，也不是很复杂。

（其实这个公式完全不需要记）

劈尖干涉、牛顿环、迈克尔孙干涉仪见另一篇文章，公式基本都可以现场推导，在此不过多赘述。

时空相干性大物B不考。

光的衍射

惠更斯-菲涅尔原理

惠更斯：子波

菲涅尔：子波相干叠加

具体公式没标重点，应该不会考怎么用。

夫琅禾费衍射

不太重要但不知道会不会考的公式：

I = I_0(\frac{\sin\beta}{\beta})^2\\ \beta = \frac{\pi}{\lambda}a\sin\theta

很重要的那个公式：

a\sin\theta = k\lambda\\ k=\pm1, \pm2, ...,k\ne0

这个公式描述了夫琅禾费衍射的暗纹条件。

明纹条件：

a\sin\theta = \pm\frac{2k+1}{2}\lambda\\ k=1, 2, ...,k\ne0

注意没含1/2。

宽度啥的可以现推，有的时候能用这个近似：

\sin\theta \approx \tan\theta \approx \theta

\theta_k = \arcsin\frac{k\lambda}{a} \approx \frac{k\lambda}{a}

然后透镜有个公式，以及近似：

x=f\tan\theta\approx f\theta

用这些就能够推了

圆孔衍射

艾里斑

角半径

\theta_0 = \arcsin(0.61\frac\lambda R) \approx 0.61\frac\lambda R = 1.22\frac\lambda D

其中D为孔径

艾里斑半径：

r_0 = f\tan\theta = 1.22 \frac{\lambda f} D

瑞利判据

最小分辨角（ \delta\varphi ）即为 \theta_0。

分辨本领（ R ）为最小分辨角倒数。

光栅衍射

光栅方程：

(a+b)\sin\theta = \pm k\lambda

即为明纹条件。

缺级现象就是把干涉明纹和衍射暗纹两个联立了一下。

光栅光谱

考了再写。总之只有白色一级独立。

光的偏振

光的偏振状态

完全偏振光⇔线偏振光⇔平面偏振光

部分偏振光——偏振度：

P = \frac{I_{max} - I_{min}}{I_{max}+I_{min}}

圆偏振光、椭圆偏振光：相当于垂直方向且具有固定相位差两束线偏振光叠加。

马吕斯定律

对光振动方向选择性吸收——二向色性

起偏器、检偏器——概念较为显然，不多介绍

自然光经过偏振片后，光强变为一半

马吕斯定律：

I = I_0\cos^2\alpha

注意： I_0 为线偏振光光强。

布儒斯特定律

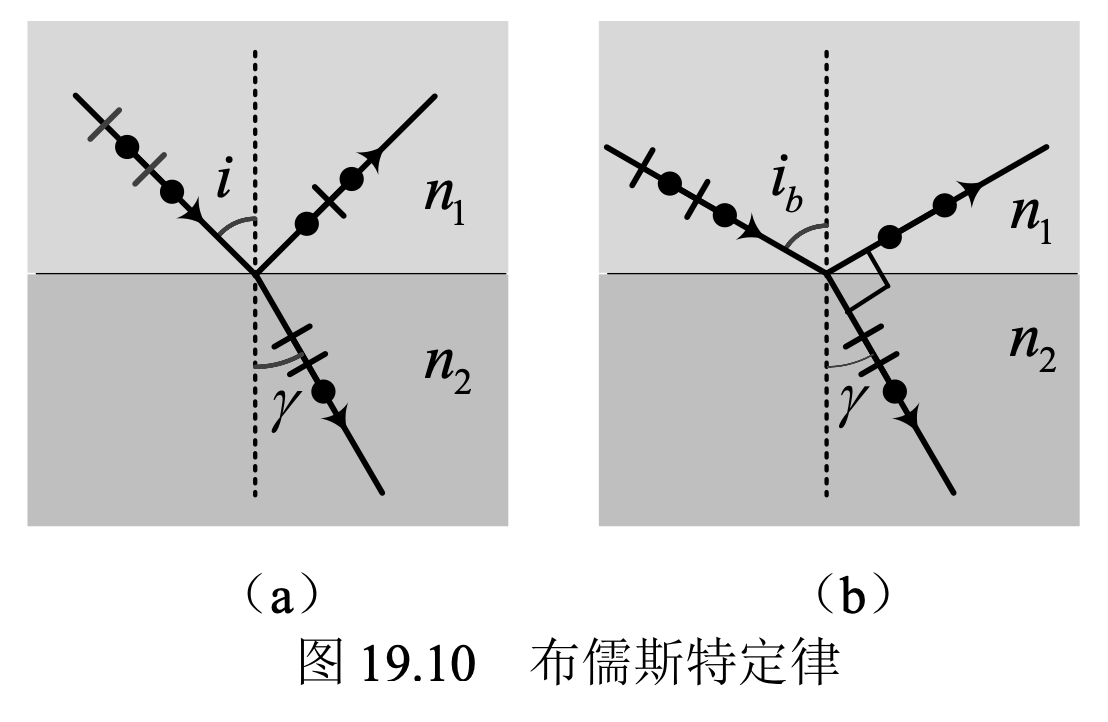
入射角满足

\tan i_B = \frac {n_2} {n_1}

反射光变为完全偏振光

i_B 为布儒斯特角/起偏角

反射线与折射线垂直

起偏——玻璃片堆，具体原理不深入。

双折射

说简单点就是会产生两束光，一个符合折射定律（o光），一个不符合折射定律（e光），o光和e光均为偏振光、偏振方向垂直……

不过这块我们老师也没怎么说，而且习题都跟波片有关，应该不会重点考察。