所有程序为笔者个人所写,仅供参考。
2023-2024
第一题(必做题)
题面
在森林上定义一种特殊的遍历次序,称为H遍历。
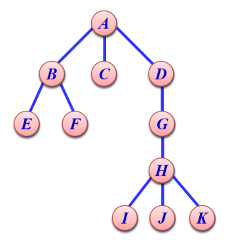
规则如下:对于有多棵子树的森林,先遍历第一棵子树T1,再遍历第二棵子树T2,依次按顺序遍历完所有子树。在每一棵子树内部,比如T1的内部,先遍历T1的第一棵子树,再访问T1的根结点,再遍历T1的其余的子树森林。
如图所示,该树的H遍历结果是:EBFACIHJKGD。
因为任意的树都可以转换为对应的二叉树,如上图所示的树,可以转换成下图所示的二叉树:
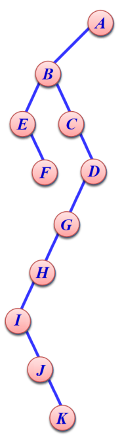
请设计一个算法,能够在以二叉链表表示的树(即孩子兄弟链结构)上输出H遍历次序。
具体要求如下:
(1) 定义二叉树的结点的数据类型,并使用动态内存分配的方式向二叉树中插入新的结点。(5分)
(2) 定义栈元素的数据类型,以满足遍历二叉链表结构的需要。概念上是一个二叉树的结点入栈,同时应该表明该结点是其父结点的左孩子还是右孩子,这样可以方便判断回溯时是从左子树上来的还是从右子树上来的。(5分)
(3) 要求该算法是非递归算法,不允许使用递归。在算法中可以使用自定义的栈,也可以使用C/C++库中的栈。(5分)
(4) 不允许将二叉链表结构改造成一般树的孩子链结构,也就是说,不允许在树上进行H遍历,而是要直接在对应的二叉树上进行H遍历。(5分)
(5) 算法执行完毕,要以正确的方式释放动态申请的空间;(5分)
(6) 在遍历二叉树的过程中,遇到左子树为空,而右子树不空的结点,要同时输出该结点及其父结点(如连续输出E、B)。(5分)
(7) 在遍历二叉树的过程中,一旦对一个结点进行退栈操作,意味着要连续对一系列的结点进行退栈操作。条件包括右子树为空或者右子树已经处理完毕,或者左子树已经处理完毕且右子树为空。(5分)
(8) 当一个结点退栈,且是从非空的左子树回溯时,如果结点的子结点没有右孩子,应当输出该结点(如输出G)。(5分)
(9) 在结点连续退栈的过程中,如果到达一个从左子树回溯的结点,且其右子树非空,则应输出其父结点的数据(如到达B,输出A)。(5分)
(10) 以本题所示的图中的树为数据,输出正确的H遍历的结果。(5分)
要求main()函数实现下述操作:
int main(){
BTNode *root;
makeTree(root);
HTravserse(root);
freeTree(root);
return 0;
}提示:本题的目的是考查如何显式使用栈来完成树上的特殊次序的深度优先遍历。因此,基本思路是在二叉树上完成深度优先遍历,在下降的过程中完成入栈的操作,在出栈的过程中确认对子树的处理结果。难点在于,一个结点退栈和输出该结点的数据并不总是同步发生的,有些结点在退栈之前就已经输出了,因此要寻找合适的输出结点数据的时机。为了防止结点重复入栈,退栈的操作应该是连续的,或者设计特殊的栈元素结构表明结点的状态。
解答
#include <iostream>
#include <stack>
using namespace std;
typedef struct BTNode {
char data;
struct BTNode* left;
struct BTNode* right;
BTNode(char data, struct BTNode* left, struct BTNode* right) {
this->data = data;
this->left = left;
this->right = right;
}
} BTNode;
void makeTree(BTNode* &root) {
//Hard-encoded nodes
BTNode* r = new BTNode('K',nullptr,nullptr);
r = new BTNode('J',nullptr,r);
r = new BTNode('I',nullptr,r);
r = new BTNode('H',r,nullptr);
r = new BTNode('G',r,nullptr);
r = new BTNode('D',r,nullptr);
r = new BTNode('C',nullptr,r);
BTNode* l = new BTNode('F',nullptr,nullptr);
l = new BTNode('E',nullptr,l);
r = new BTNode('B',l,r);
r = new BTNode('A',r,nullptr);
root = r;
}
typedef struct StElement {
BTNode* node;
int position;
BTNode* parent;
int status;
}StElement;
void HTravserse(BTNode* &root) {
stack<StElement> s;
s.push(StElement{root,1,nullptr,0});
while(!s.empty()) {
StElement &p = s.top();
if (p.node==nullptr) {
if (p.position==0&&p.parent!=nullptr) {
cout<<p.parent->data<<" ";
}
s.pop();
continue;
}
if (p.status == 0) {
s.push(StElement{p.node->left,0,p.node,0});
p.status = 1;
continue;
}
if (p.status == 1) {
if (p.position==0) {
cout<<p.parent->data<<" ";
BTNode* r = p.node->right;
s.pop();
stack<StElement> ss;
while (r!=nullptr) {
ss.push(StElement{r,1,p.node,0});
r = r->right;
}
while (!ss.empty()) {
s.push(ss.top());
ss.pop();
}
} else {
s.pop();
}
}
}
}
void freeTree(BTNode* root) {
if (root==nullptr) return;
freeTree(root->left);
freeTree(root->right);
delete root;
}
int main() {
BTNode* root;
makeTree(root);
HTravserse(root);
freeTree(root);
return 0;
}重点就是栈中的每个节点有两个标记,明确这个就很好写了。
第二题(选做题)
题面
对n 个不同的正整数,进行如下操作:每一次删去其中两个数 a 和 b,然后加入一个新数:a*b+1,如此循环操作直到只剩下一个数。所有按这种操作方式最后得到的数中,最大的为max,最小的为min,计算max-min。
举例如下:假设有三个数 2,4,3。
第一种循环操作:取出4,3,将4*3+1放回序列,得到2,13;2*13+1=27。
第二种循环操作,取出2,3,将2*3+1放回序列,得到4,7;4*7+1=29。
所以,max-min=29-27=2。
定理:每次从序列中取出两个最小的整数,循环操作可以得到max。每次从序列中取出两个最大的整数,循环操作可以得到min。
根据以上定理(定理已经给出,无需证明),编写一个算法得到一个正整数序列上的max-min的值。具体要求如下:
(1) 程序运行时,从键盘上输入序列长度n,以及n个正整数值。(10分)
(2) 采用合适的数据结构,完成对max和min的计算。(20分)
(3) 所采用的数据结构,可以自己编写,也可以使用C/C++中的库函数或者类。(10分)
(4) 输入多个不同的序列,都能够得到正确的结果。(5分)
(5) 使用int类型的变量,序列长度逐渐增加,程序运行会得到错误的结果,是何原因,如何解决?(3分)
(6) 在序列长度为n的情况下,分析算法复杂度。(2分)
解答
#include <iostream>
#include <queue>
using namespace std;
int main() {
int n;
cin>>n;
priority_queue<int,vector<int>,less<>> q_min;
priority_queue<int,vector<int>,greater<>> q_max;
for (int i=0; i<n; i++) {
int input;
cin>>input;
q_min.push(input);
q_max.push(input);
}
while (q_max.size()!=1) {
int a = q_max.top();
q_max.pop();
int b = q_max.top();
q_max.pop();
q_max.push(a*b+1);
}
while (q_min.size()!=1) {
int a = q_min.top();
q_min.pop();
int b = q_min.top();
q_min.pop();
q_min.push(a*b+1);
}
cout<< q_max.top() - q_min.top() <<endl;
return 0;
}大水题,会优先队列就能解。
第三题(选做题)
题面
给定一个后缀表达式,如ab+c*d+e*,将其转换成对应的中缀表达式,如((a+b)*c+d)*e。
为简化编程,所有的运算数直接用单个字母表示,运算符只有+、-、*、/四种。具体要求如下:
(1) 在中缀表达式中,考虑到运算符之间的优先级,在有需要使用括号()时,必须使用;
(2) 没有必要使用括号时,不允许出现多余的括号;
(3) 输入的后缀表达式是一个字符串,输出的中缀表达式也要求是一个字符串;(5分)
(4) 自行选用合适的辅助数据结构,如栈、队列等。这些辅助数据结构可以自行实现,也可以调用C/C++函数库或者类库;(10分)
(5) 正确处理空间的申请和释放;(5分)
(6) 输入的后缀表达式有可能是非法的,要能识别表达式是否非法;(5分)
(7) 正确组织处理流程,输出的结果正确无误;(20分)
(8) 在不同的表达式上都取得正确的结果。(5分)
解答
#include <iostream>
using namespace std;
int parse_operand(string s) {
int ops = 0;
int vals = 0;
for (int i = 0; i < s.length(); i++) {
if (s[i]>='0' && s[i]<='9') {
vals++;
} else if (s[i]=='+' || s[i]=='-' || s[i]=='*' || s[i]=='/') {
ops++;
}
else throw runtime_error("Invalid character!");
if (vals == ops+1) {
return i;
}
}
throw runtime_error("Invalid sequence!");
}
pair<string,char> translate(string s) {
if (s.empty()) throw runtime_error("Invalid syntax!");
char ch = s[0];
if (ch>='0' && ch<='9' && s.size() == 1) {
return {string({ch}),ch};
} else if (s.size()<2) {
throw runtime_error("Invalid syntax!");
} else if (ch=='+' || ch=='-') {
int split = parse_operand(s.substr(1));
return {translate(s.substr(2+split)).first + ch + translate(s.substr(1,1+split)).first,'+'};
} else if (ch=='*' || ch=='/') {
int split = parse_operand(s.substr(1));
pair<string,char> r1 = translate(s.substr(1,1+split));
pair<string,char> r2 = translate(s.substr(2+split));
return {((r2.second=='+' || r2.second == '-') ?"(":"") +
r2.first +
((r2.second=='+' || r2.second == '-') ?")":"") +
ch +
((r1.second=='+' || r1.second == '-') ?"(":"") +
r1.first +
((r1.second=='+' || r1.second == '-') ?")":"")
,'-'};
}
throw runtime_error("Invalid sequence!");
}
int main() {
string s;
cin >> s;
reverse(s.begin(), s.end());
try {
cout<<translate(s).first<<endl;
} catch (exception &e) {
cout << "[ERROR] " << e.what() << endl;
}
return 0;
}没什么特别好说的,就是一个递归,这里的异常处理用的是try-catch。
2022-2023
题面

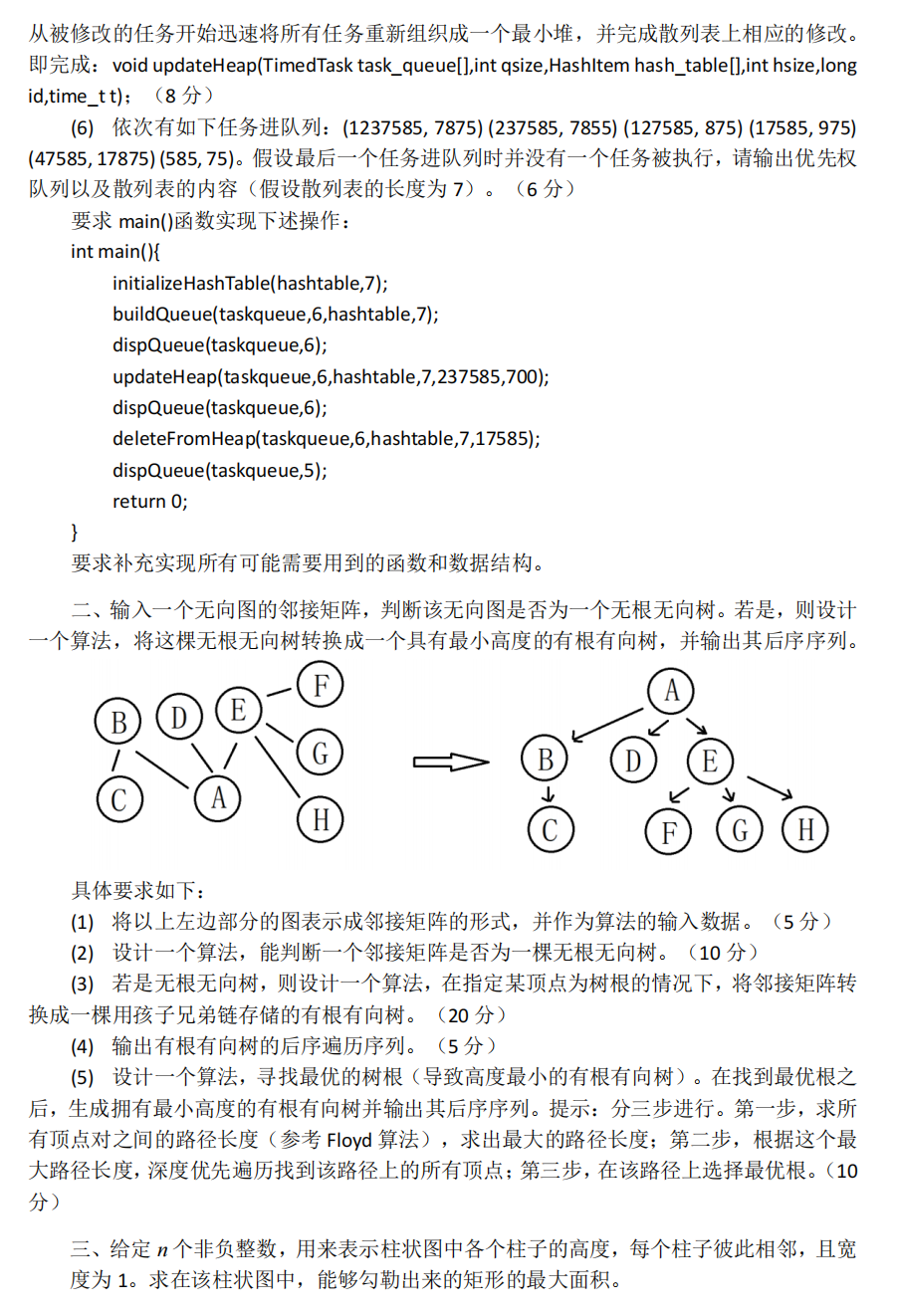

解答
第一题
#include <iostream>
#include <set>
using namespace std;
class TimedTask {
public:
long id;
time_t t;
TimedTask(long id,time_t time) {
this->id=id;
this->t=time;
}
//这里我使用重载运算符的方式去处理排序的问题
bool operator>(TimedTask &task) const {
return this->t>task.t;
}
bool operator<(TimedTask &task) const {
return this->t<task.t;
}
bool operator<=(TimedTask &task) const {
return this->t<=task.t;
}
bool operator>=(TimedTask &task) const {
return this->t>=task.t;
}
};
struct HashItem {
long key;
int id;
};
//抄的OI-Wiki的板子,课本上的板子就是一坨
int& getHT(HashItem *ht,int h_size,long n) {
long idx = (n%h_size+h_size)%h_size;
int cnt = 1;
while (ht[idx].key != n && ht[idx].id != -1) {
idx = (idx+cnt)%h_size;
cnt++;
}
ht[idx].key = n;
return ht[idx].id;
}
bool adjustUp(TimedTask task_queue[],int qsize,int pos,HashItem hash_table[],int hsize) {
bool flag=false;
while (pos > 1 && task_queue[pos] < task_queue[pos / 2]) {
getHT(hash_table,hsize,task_queue[pos].id) = pos/2;
getHT(hash_table,hsize,task_queue[pos/2].id) = pos;
swap(task_queue[pos], task_queue[pos / 2]);
flag = true;
pos /= 2;
}
return flag;
}
bool adjustDown(TimedTask task_queue[],int qsize,int pos,HashItem hash_table[],int hsize) {
bool flag=false;
while (pos * 2 <= qsize) {
int t = pos * 2;
if (t + 1 <= qsize && task_queue[t + 1] < task_queue[t]) t++;
if (task_queue[t] >= task_queue[pos]) break;
getHT(hash_table,hsize,task_queue[pos].id) = t;
getHT(hash_table,hsize,task_queue[t].id) = pos;
swap(task_queue[pos], task_queue[t]);
flag = true;
pos = t;
}
return flag;
}
void initializeHashTable(HashItem* h,int size) {
for (int i=0;i<size;i++) {
h[i].id = -1;
}
}
void buildQueue(TimedTask* q,int q_size,HashItem* h,int h_size) {
for (int i=1;i<=q_size;i++) {
getHT(h,h_size,q[i].id) = i;
}
for (int i=q_size;i>0;i--) {
adjustDown(q,q_size,i,h,h_size);
}
}
void dispQueue(TimedTask* q,int q_size) {
for (int i=1;i<=q_size;i++) {
cout<<q[i].id<<" "<<q[i].t<<endl;
}
cout<<endl;
}
void updateHeap(TimedTask* q,int q_size,HashItem* h,int h_size,long id,time_t time) {
int i = getHT(h,h_size,id);
time_t prev = q[i].t;
q[i].t = time;
if (time<prev) {
adjustUp(q,q_size,i,h,h_size);
} else {
adjustDown(q,q_size,i,h,h_size);
}
}
void deleteFromHeap(TimedTask* q,int q_size,HashItem* h,int h_size,long id) {
int& ht = getHT(h,h_size,id);
int i = ht;
time_t prev = q[i].t;
time_t time = q[q_size].t;
getHT(h,h_size,q[q_size].id) = i;
swap(q[i],q[q_size]);
if (time<prev) {
adjustUp(q,q_size-1,i,h,h_size);
} else {
adjustDown(q,q_size-1,i,h,h_size);
}
ht = -1;
}
int main () {
HashItem hashtable[7];
TimedTask taskqueue[7] = {
TimedTask(0,0),
TimedTask{1237585,7875},
TimedTask{237585,7855},
TimedTask{127585,875},
TimedTask{17585,975},
TimedTask{47585,17875},
TimedTask{585,75}
};
initializeHashTable(hashtable,7);
buildQueue(taskqueue,6,hashtable,7);
dispQueue(taskqueue,6);
updateHeap(taskqueue,6,hashtable,7,237585,700);
dispQueue(taskqueue,6);
deleteFromHeap(taskqueue,6,hashtable,7,17585);
dispQueue(taskqueue,5);
return 0;
}第二题
#include <iostream>
#define M 8
#define MAX 10000
using namespace std;
//图的邻接矩阵
int mat[M][M];
//二叉树
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
};
//建孩子兄弟链的二叉树,代码思路应该比较清楚
TreeNode* makeTree(vector<bool> &visited,int root) {
visited[root] = true;
TreeNode *p = new TreeNode();
TreeNode* t = p;
t->val = root;
bool flag = false;
for (int i = 0; i < M; i++) {
if (mat[root][i] && !visited[i]) {
if (!flag) {
flag = true;
t->left = makeTree(visited,i);
t = t->left;
} else {
t->right = makeTree(visited,i);
t = t->right;
}
}
}
return p;
}
TreeNode* makeTree(int root) {
vector<bool> v = vector<bool>(M,false);
return makeTree(v,root);
}
void destroyTree(TreeNode* node) {
if (node == nullptr)return;
destroyTree(node->left);
destroyTree(node->right);
delete node;
}
void traverse(TreeNode* node) {
if (node == nullptr)return;
TreeNode* p = node->left;
while (p != nullptr) {
traverse(p);
p = p->right;
}
cout << char(node->val + 'A') << endl;
}
//图上dfs
int dfs(vector<bool> &visited,int node) {
visited[node] = true;
int max = 1;
for (int i = 0; i < M; i++) {
if (mat[node][i] && !visited[i]) {
int d = dfs(visited,i)+1;
max = max > d ? max : d;
}
}
return max;
}
int findMinRoot() {
vector<vector<int>> dist = vector<vector<int>>(M,vector<int>(M,0));
vector<vector<int>> path = vector<vector<int>>(M,vector<int>(M,-1));
for (int i = 0; i < M; i++) {
for (int j = 0; j < M; j++) {
if (i!=j) dist[i][j] = mat[i][j]==1?1:MAX;
else dist[i][j] = 0;
if (i!=j&&mat[i][j]==1) {
path[i][j] = i;
} else {
path[i][j] = -1;
}
}
}
for (int k = 0; k < M; k++) {
for (int i = 0; i < M; i++) {
for (int j = 0; j < M; j++) {
if (dist[i][j] > dist[i][k] + dist[k][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
path[i][j] = path[k][j];
}
}
}
}
//以上是抄的教材的Floyd板子
//接下来寻找最长路径
int maxi=-1,maxj=-1,maxn=0;
for (int i = 0; i < M; i++) {
for (int j = 0; j < M; j++) {
if (dist[i][j] > maxn && path[i][j] != -1) {
maxn = dist[i][j];
maxi = i;
maxj = j;
}
}
}
//然后抄Floyd的输出板子,但是加了个图上dfs去找最矮的树
vector<bool> visited(M,false);
int min = dfs(visited,maxj);
int mini = maxj;
//cout <<mini<<" "<< min << endl;
int end = path[maxi][maxj];
//cout<<maxj<<" ";
int begin = maxi;
while (end != maxi) {
visited = vector<bool>(M,false);
int d = dfs(visited,end);
if (d<min) {
min = d;
mini = end;
//cout <<mini<<" "<< min << endl;
}
end = path[begin][end];
}
visited = vector<bool>(M,false);
int d = dfs(visited,begin);
if (d<min) {
min = d;
mini = begin;
//cout <<mini<<" "<< min << endl;
}
//cout << maxn <<" "<< maxi<<" "<<maxj << endl;
return mini;
}
int main() {
int div = 0;
for (int i=0;i<M;i++) {
for (int j=0;j<M;j++) {
cin >> mat[i][j];
if (i != j) div += mat[i][j];
}
}
if (div!=(M-1)*2) {
cout<<"Not a tree!"<<endl;
return 0;
}
TreeNode* node = makeTree(findMinRoot());
traverse(node);
cout << endl;
destroyTree(node);
return 0;
}第三题
这题和LeetCode的接雨水很像,主要是分析清楚题目要做的实际上是不断寻找最左侧第一个比当前位置小的所有节点。
#include <iostream>
#define N 1005
using namespace std;
int st[N];
int top = -1;
int max(int a,int b) {
if (a>b) return a;
return b;
}
int maxRectangle(int A[],int n) {
int maxn = A[0];
for (int i = 0; i < n; i++) {
if (top == -1) {
st[++top] = i;
} else {
while (A[st[top]]>A[i] && top != -1) {
top--;
}
st[++top] = i;
for (int j=top;j>=0;j--) {
maxn = max(maxn,(i-st[j]+1)*A[st[j]]);
}
}
}
return maxn;
}
int main() {
int n;
cin >> n;
int A[N];
for (int i=0;i<n;i++) {
cin>>A[i];
}
cout<<maxRectangle(A, n)<<endl;
return 0;
}2021-2022
题面



解答
感觉除了必做题(第一题),是近几年最温柔的一套题了。
(实际上第一题也很温柔)
第一题
#include <iostream>
#include <list>
using namespace std;
int Graph[9][9] = {
{0,0,1,0,0,0,0,1,0},
{0,0,1,1,1,0,0,0,0},
{0,0,0,1,0,0,0,0,0},
{0,0,0,0,0,1,1,0,0},
{0,0,0,0,0,1,0,0,0},
{0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,1},
{0,0,0,0,0,0,1,0,0}
};
int InDegree[25];
int Path[25];
int ZS[25];
void calculateInDegree(int graph[][9],int inDegree[]) {
for (int i=0;i<9;i++) {
for (int j=0;j<9;j++) {
if (graph[i][j]==1) {
inDegree[j]++;
}
}
}
}
void topSort(int graph[][9],int inDegree[],int path[],int zs[],int& top,int k,int p,int& cnt) {
path[k++] = p;
if (k==9) {
cnt++;
cout << cnt <<":";
for (int i=0;i<9;i++) {
cout << " C"<<1+path[i];
if (i!=8) cout << ",";
}
cout<<endl;
} else {
for (int i=0;i<9;i++) {
if (graph[p][i]) {
inDegree[i]--;
if (inDegree[i]==0) {
zs[++top] = i;
}
}
}
for (int i=0;i<=top;i++) {
bool flag = false;
for (int j=0;j<k;j++) {
if (path[j] == zs[i])flag = true;
}
if (!flag) topSort(graph,inDegree,path,zs,top,k,zs[i],cnt);
}
for (int i=0;i<=top;i++) {
if (graph[p][zs[i]]) {
swap(zs[i],zs[top]);
top--;
i--;
}
}
for (int i=0;i<9;i++) {
if (graph[p][i]) {
inDegree[i]++;
}
}
}
}
void topSort(int graph[][9],int inDegree[],int path[],int zs[],int k) {
int top = -1;
bool flag = false;
for (int i=0;i<9;i++) {
if (inDegree[i]==0) {
zs[++top] = i;
flag = true;
}
}
if (!flag) {
cout<<"没有拓扑序列"<<endl;
return;
}
int cnt = 0;
for (int i=0;i<=top;i++) {
topSort(graph,inDegree,path,zs,top,k,zs[i],cnt);
}
if (cnt == 0) {
cout<<"没有拓扑序列"<<endl;
}
}
int main() {
calculateInDegree(Graph,InDegree);
topSort(Graph,InDegree,Path,ZS,0);
return 0;
}第二题
#include <iostream>
#include <cstdio>
using namespace std;
void makeGraph(vector<vector<int>> &graph,int m) {
for (int i=0;i<m;i++) {
int x,y;
cin>>x>>y;
graph[x].push_back(y);
graph[y].push_back(x);
}
}
int bfsOnVertex(vector<vector<int>> &graph,int v,int maxDepth) {
int n = graph.size()-1;
queue<pair<int,int>> q;
vector<bool> visited(n+1,false);
q.push({v,0});
while (!q.empty()) {
int vertex = q.front().first;
int depth = q.front().second;
visited[vertex] = true;
q.pop();
for (int &vtx : graph[vertex]) {
if (!visited[vtx] && depth <= maxDepth-1) {
q.push({vtx,depth+1});
}
}
}
int cnt = 0;
for (int i=1;i<=n;i++) {
if (visited[i]) cnt++;
}
return cnt;
}
void calculateDists(vector<vector<int>> &graph,int maxDist) {
int n = graph.size()-1;
for (int i=1;i<=n;i++) {
printf("%4.2f%%\n",((float)bfsOnVertex(graph,i,maxDist)/(float)n)*100);
}
}
int main() {
int n,m;
cin>>n>>m;
vector<vector<int>> graph(n+1);
makeGraph(graph,m);
calculateDists(graph,6);
return 0;
}这题的题目描述有点问题,最后总人数如果按N-1计算的话,和样例输出不符。这里以样例输出为准。
第三题
#include <iostream>
using namespace std;
struct BTNode {
int data = -1;
BTNode *left = nullptr;
BTNode *right = nullptr;
BTNode(int data) {
this->data = data;
}
};
void makeTree(BTNode* &root) {
root = new BTNode(1);
root->left = new BTNode(2);
root->right = new BTNode(3);
root->left->left = new BTNode(4);
root->left->right = new BTNode(5);
root->right->left = new BTNode(6);
root->left->left->right = new BTNode(7);
}
int calculateMaxWidth(BTNode *root) {
queue<pair<BTNode*,int>> q;
q.emplace(root,0);
int currentDepth = -1;
int width = 0;
int maxWidth = 0;
while (!q.empty()) {
pair<BTNode*,int> p = q.front();
q.pop();
if (currentDepth == p.second) {
width++;
} else {
maxWidth = max(maxWidth,width);
width = 1;
currentDepth = p.second;
}
if (p.first->left != nullptr) {
q.emplace(p.first->left,p.second+1);
}
if (p.first->right != nullptr) {
q.emplace(p.first->right,p.second+1);
}
}
maxWidth = max(maxWidth,width);
return maxWidth;
}
void destroyTree(BTNode *&root) {
if (root == nullptr) return;
destroyTree(root->left);
destroyTree(root->right);
delete root;
}
int main() {
BTNode *root = nullptr;
makeTree(root);
cout << calculateMaxWidth(root) << endl;
destroyTree(root);
return 0;
}
